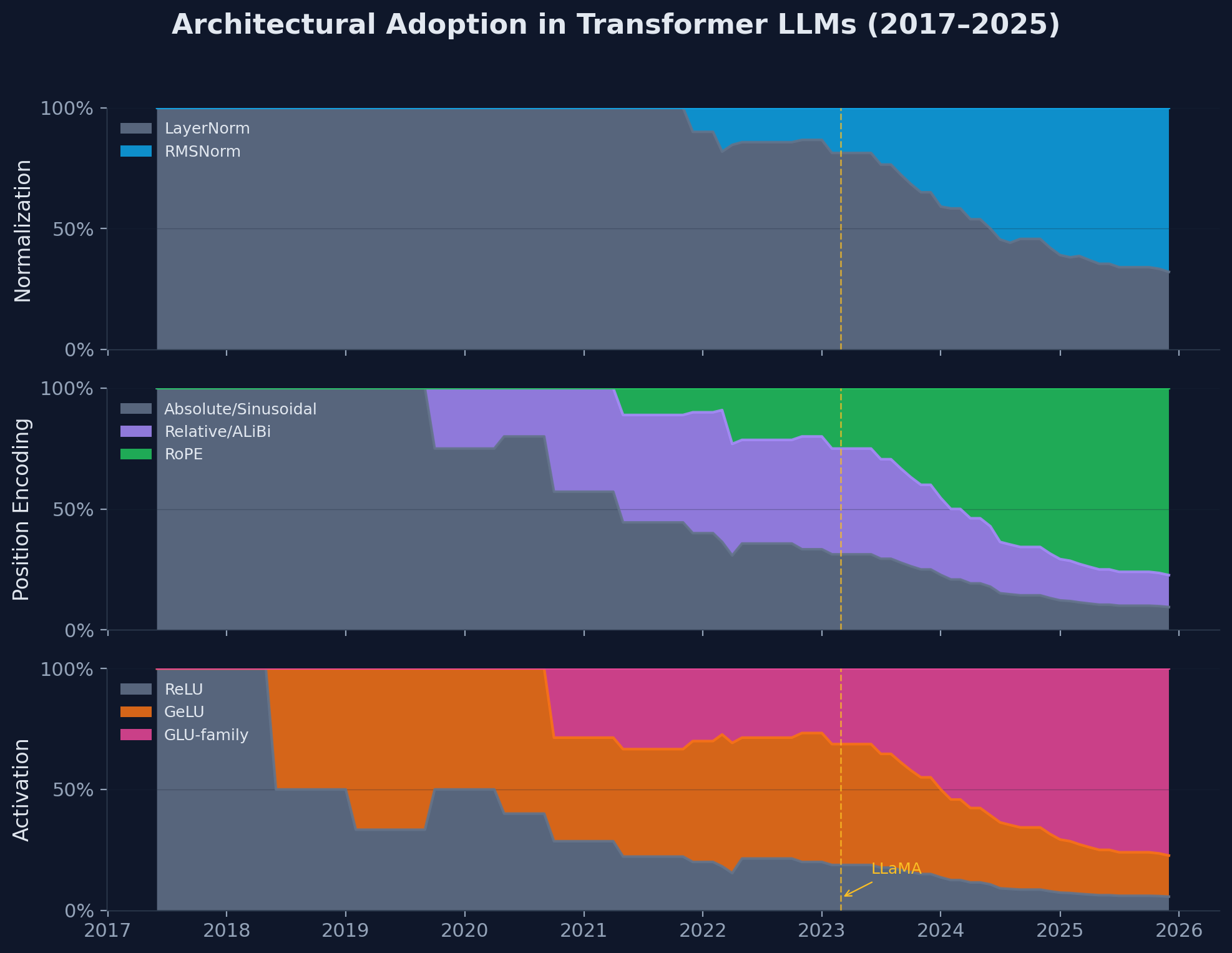
Between 2017 and 2025, transformer architectures for LLMs underwent rapid exploration followed by striking convergence. This article traces decisions across 53 models and identifies a de facto 2023–2025 stack: pre-norm (RMSNorm), RoPE, SwiGLU MLPs, KV-sharing (MQA/GQA), and bias-free layers. We discuss both model-intrinsic factors (optimization stability, quality-per-FLOP) and practical constraints (kernel availability, KV-cache economics). Diversity persists mainly in MoE routing and long-context attention. The accompanying dataset records publication dates and architectural specs.

#Convergence as Signal

In June 2017, [4] introduced the transformer with a specific set of architectural choices: post-layer normalization, sinusoidal position encodings, ReLU activations, and 4x MLP expansion. Each choice was reasonable but not obviously optimal. The subsequent eight years saw extensive experimentation with alternatives.

By 2024, many influential open-weight decoder-only model families converged on a similar bundle: pre-norm (often RMSNorm), RoPE-family position encodings, GLU-family MLPs (commonly SwiGLU with parameter-matched width), and KV-sharing attention variants (MQA/GQA). Several also drop most bias terms (sometimes keeping QKV-only biases). This is not literally universal, as there are notable hybrids and counter-trends (e.g., ALiBi/relative-bias lineages, RoPE+NoPE mixtures, and nonstandard norm stacks), but the center of mass is clear. The original transformer's choices were replaced wholesale.

When many independent groups converge on similar design choices, it is evidence of a strong shared basin of solutions. But convergence can also reflect common constraints (hardware/software stacks, kernel availability, inference economics) and path dependence (influential released checkpoints and reference implementations). The goal here is to separate what appears robust from what may be contingent.

This article examines the architectural evolution through three lenses:

1. Historical progression: How did we get from the 2017 transformer to the 2025 consensus? What problems did each innovation solve?

2. Technical foundations: What mathematical properties make RoPE more attractive to learned absolute positions? Why does SwiGLU outperform GeLU despite having fewer effective parameters? Why does QK-normalization stabilize training?

3. Remaining frontiers: Where has convergence not occurred? What does ongoing architectural diversity in MoE configurations, attention patterns, and stability mechanisms tell us about unsolved problems?

Scope note: "convergence" here is primarily about dense, decoder-only LLM blocks (norm/pos-enc/MLP/attention) rather than training recipe, data, post-training, or system-level inference tricks. The dataset is "widely discussed models", which tilts toward models with public technical reports and/or open weights.

The analysis draws on a dataset of 53 transformer LLMs spanning 2017-2025, with architectural specifications cross-referenced against primary sources.

#Four Eras of Transformer Architecture

The evolution of transformer LLMs divides naturally into four eras, each characterized by distinct architectural priorities and innovations.

#Era I: Foundations (2017-2019)

The original transformer established the fundamental structure that persists today: alternating multi-head self-attention and position-wise feed-forward layers, connected by residual streams. The specific implementation choices, however, were largely inherited from prior work or chosen for simplicity.

Normalization placement followed the convention from residual networks: apply normalization after the residual addition (post-norm). For a sublayer function $f$ (attention or FFN), the computation was:

$$x_{l+1}=\text{LayerNorm}(x_l+f(x_l))$$

Position encoding used fixed sinusoidal functions, encoding absolute position $p$ in dimension $i$ as:

$$P{E}_{(p,2i)}=\sin (p/10000^{2i/d})$$ $$P{E}_{(p,2i+1)}=\cos (p/10000^{2i/d})$$

This choice was elegant, requiring no learned parameters and theoretically enabling length generalization through the linear properties of sinusoids, but subsequent work showed learned absolute positions performed better in practice.

Feed-forward networks used the standard MLP structure with ReLU activation and 4x expansion:

$$\text{FFN}(x)=\max (0,x{W}_1+b_1)W_2+b_2$$

where $W_1\in {\mathbb{R}}^{d\times 4d}$ and $W_2\in {\mathbb{R}}^{4d\times d}$.

GPT-1 (2018) moved to decoder-only architecture with learned absolute positions and GeLU activation. GPT-2 (2019) introduced the critical shift to pre-normalization:

$$x_{l+1}=x_l+f(\text{LayerNorm}(x_l))$$

This change is widely associated with improved optimization stability at depth. One intuition is gradient flow: in post-norm, gradients repeatedly pass through normalization in the main residual pathway; in pre-norm, the residual stream provides a cleaner identity path while normalization shapes only the sublayer contribution.

#Era II: Scale-Up (2020-2022)

The GPT-3 moment demonstrated that scaling (simply training larger models on more data) produced qualitative capability improvements. This era focused on enabling efficient scaling through architectural refinements.

RMSNorm (Root Mean Square Layer Normalization), introduced by Zhang & Sennrich (2019), gained traction in this period when it was adopted by Gopher and Chinchilla. Standard LayerNorm computes:

$$\text{LayerNorm}(x)=\frac{x-\mu }{\sigma }\odot \gamma +\beta$$

where $\mu$ and $\sigma$ are the mean and standard deviation across features. RMSNorm simplifies this by removing the mean-centering:

$$\text{RMSNorm}(x)=\frac{x}{\text{RMS}(x)}\odot \gamma ,\text{RMS}(x)=\sqrt{\frac{1}{d}\sum _{i=1}^d{x}_i^2}$$

The computational savings are modest (often reported around 10-15%, implementation-dependent), but empirically RMSNorm matches LayerNorm in many transformer settings while simplifying the normalization operation. Mean-centering is not "wrong" per se, but it often appears unnecessary for good training dynamics in modern pre-norm transformers, and removing it can slightly improve efficiency.

Parallel attention and FFN was introduced by GPT-J, GPT-NeoX, and later PaLM. Instead of sequential computation:

$$x_l^{\prime }=x_l+\text{Attn}(\text{Norm}(x_l)),x_{l+1}=x_l^{\prime }+\text{FFN}(\text{Norm}(x_l^{\prime }))$$

the parallel formulation computes both sublayers from the same input and sums:

$$x_{l+1}=x_l+\text{Attn}(\text{Norm}(x_l))+\text{FFN}(\text{Norm}(x_l))$$

This can improve hardware utilization by increasing parallelizable work; reported speedups vary by implementation, model shape, and kernel support, but are often on the order of ~10-20% with minimal quality impact.

Rotary Position Embeddings (RoPE) were introduced by Su et al. (2024) and quickly adopted by GPT-J, GPT-NeoX, and PaLM. We defer detailed analysis to Section 3.1, but the key innovation is encoding relative position information through rotation matrices applied to query and key vectors, rather than adding absolute position embeddings to the input.

SwiGLU activation was introduced by Shazeer (2020) and later adopted at scale by PaLM. The technique builds on the Gated Linear Unit family. The standard FFN:

$$\text{FFN}(x)=\text{GeLU}(x{W}_1)W_2$$

becomes:

$$\text{SwiGLU}(x)=(\text{SiLU}(x{W}_1)\odot x{W}_3)W_2$$

where SiLU (Swish) is $x\cdot \sigma (x)$ and $\odot$ denotes element-wise multiplication. The gating mechanism ($x{W}_3$) modulates the activated representation, improving expressivity. However, the third weight matrix increases parameters, so the hidden dimension is reduced from $4d$ to $\frac{8d}{3}$ to maintain parameter count.

#Era III: Efficiency and Open Source (2023-2024)

LLaMA (February 2023) crystallized the modern architecture. While each component existed before, LLaMA's combination (and Meta's decision to release weights) established a reproducible baseline that virtually all subsequent open models adopted.

The LLaMA recipe is as such:

This recipe succeeded because it simultaneously optimized multiple objectives: training stability, inference efficiency, implementation simplicity, and model quality. The absence of bias terms, for instance, slightly improves training dynamics and simplifies the implementation without measurable quality loss.

Grouped-Query Attention (GQA) addressed the inference bottleneck. In standard multi-head attention (MHA), each head maintains separate key and value projections. For a model with $h$ heads, this means $h$ separate KV pairs must be cached during autoregressive generation. GQA groups multiple query heads to share single key-value heads:

$$\text{GQA}:Q\in {\mathbb{R}}^{h_q\times d_k},K,V\in {\mathbb{R}}^{h_{kv}\times d_k}$$

where $h_q>h_{kv}$ (typically $h_q/h_{kv}=4$ or $8$). This reduces KV-cache memory by the grouping factor with minimal quality degradation, enabling longer contexts and larger batch sizes at inference.

Vocabulary expansion accelerated during this era. LLaMA used 32K tokens, LLaMA 2 maintained this. LLaMA 3 expanded to 128K, and Gemma uses 256K. Larger vocabularies improve tokenization efficiency (fewer tokens per word, especially for non-English languages and code) at the cost of larger embedding matrices. The trend reflects both improved tokenizer algorithms (BPE variants, BBPE) and recognition that embedding parameters are relatively cheap compared to transformer layers.

Stability mechanisms emerged as models scaled:

#Era IV: MoE Dominance (2024-2025)

Dense scaling, or simply increasing model parameters, encounters diminishing returns. Training compute scales linearly with parameters, but quality improvements become sublinear. Mixture-of-Experts (MoE) provides a different scaling axis: increase total parameters while keeping active (per-token) parameters constant.

Mixtral 8×7B (January 2024) demonstrated that open MoE models could match dense models of much larger active parameter count. The architecture replaces each FFN with a routed mixture:

$$\text{MoE}(x)=\sum _{i=1}^k{g}_i(x)\cdot E_i(x)$$

where $E_i$ are expert networks (typically standard FFNs), $g_i(x)$ are routing weights from a learned router, and $k$ is the number of active experts per token (typically 1-2 for Mixtral, up to 8 for later models).

The expert scaling trajectory over 2024-2025 is dramatic:

Model	Date	Total Params	Active Params	Experts	Active
Mixtral 8×7B	Jan 2024	46.7B	12.9B	8	2
DeepSeek V3	Dec 2024	671B	37B	256+1	8
Llama 4 Maverick	Apr 2025	400B	17B	128+1	varies
Kimi K2	Jul 2025	1.04T	32B	384	8

Auxiliary-loss-free load balancing (DeepSeek V3) solved a persistent MoE training problem. Traditional approaches add an auxiliary loss to encourage balanced expert utilization:

$${\mathcal{L}}_{\text{aux}}=\alpha \sum _{i=1}^n{f}_i\cdot P_i$$

where $f_i$ is the fraction of tokens routed to expert $i$ and $P_i$ is the average routing probability for expert $i$. This loss encourages balance but distorts the primary training objective.

DeepSeek's innovation introduces a bias term $b_i$ used for selection (to maintain load balance) but excluded from the mixture weights used to form the output. Concretely, experts are selected by $s_i=r_i(x)+b_i$, but the output weights are computed from the unbiased router scores $r_i(x)$ over the selected set (formalized below in Section 3.3).

Shared experts (DeepSeek, Trinity, Llama 4) designate one or more experts as always-active, providing a stable baseline that all tokens access. This improves training stability and ensures common knowledge isn't fragmented across specialized experts.

Multi-head Latent Attention (MLA) (DeepSeek V3, Kimi K2) addresses the MoE memory challenge. With hundreds of experts, KV-cache becomes prohibitive. MLA compresses the KV representation through learned down-projections:

$$K=W_{UK}(W_{DKV}x),V=W_{UV}(W_{DKV}x)$$

where $W_{DKV}$ projects to a low-dimensional latent space, and $W_{UK},W_{UV}$ reconstruct keys and values. This dramatically reduces cache memory while preserving attention expressivity.

#2.5 Hardware Co-Evolution

Architectural convergence cannot be understood in isolation from hardware constraints. Several "winning" choices align closely with GPU/TPU optimization opportunities:

• FlashAttention [5] made $O(n^2)$ attention practical for longer sequences by restructuring memory access patterns. This reduced the urgency of linear attention research and made long-context training cheaper, increasing the value of position schemes (including RoPE) that behave well under extrapolation. RoPE is also implementation-friendly: its per-position rotations compose cleanly with common fused-attention kernels.

• Tensor core tile sizes (16×16 on A100, 8×8 on H100 for FP8) favor hidden dimensions and head counts that are multiples of these values. The near-universal choice of $d_{head}=128$ reflects this constraint as much as any quality consideration.

• Memory bandwidth bottlenecks during autoregressive inference push toward KV-cache reduction (MQA/GQA) independently of training quality. A technique that is neutral during training but reduces inference memory by 4-8× will be adopted even if it slightly hurts perplexity.

• Fused kernel availability creates path dependence: once FlashAttention, fused RMSNorm, and fused SwiGLU kernels exist and are well-optimized, switching to alternatives incurs engineering cost beyond any quality trade-off. The LLaMA recipe's dominance is partly a network effect - it's what the kernels support best.

This hardware-architecture coupling means that "convergence" partly reflects what is fast on current accelerators, not only what is best in an abstract sense. A different hardware landscape (e.g., higher memory bandwidth, different tile sizes) might favor different architectural choices.

#Technical Deep Dives

#RoPE: Why Rotation Encodes Relation

Rotary Position Embeddings (RoPE) have become the dominant default for position encoding in modern LLMs. Understanding why requires examining how position information enters the attention computation.

In standard attention, the relevance of position $m$ to position $n$ is determined by the dot product $q_n^T{k}_m$. For positions to influence attention, position information must be embedded in $q$ and $k$.

Absolute position embeddings add a position vector to the input:

$$q_n=W_q(x_n+p_n),k_m=W_k(x_m+p_m)$$

The dot product expands to four terms mixing content and position:

$$q_n^T{k}_m=(W_q{x}_n{)}^T(W_k{x}_m)+(W_q{x}_n{)}^T(W_k{p}_m)+(W_q{p}_n{)}^T(W_k{x}_m)+(W_q{p}_n{)}^T(W_k{p}_m)$$

Absolute embeddings can learn relative patterns (GPT-2 and GPT-3 demonstrated this empirically) but the architecture must learn to extract relative information from the interaction of absolute positions. RoPE instead provides a direct inductive bias: relative position enters via a simple algebraic identity, requiring no learning to achieve relative sensitivity. This also interacts favorably with length extrapolation techniques.

RoPE's insight is to encode position through rotation. For a 2D subspace of the query/key vectors, apply a rotation by angle $n\theta$:

$$R_n=\left(\begin{array}{cc}\cos n\theta & -\sin n\theta \\ \sin n\theta & \cos n\theta \end{array}\right)$$ $$q_n=R_n{W}_q{x}_n,k_m=R_m{W}_k{x}_m$$

The dot product becomes:

$$q_n^T{k}_m=(W_q{x}_n{)}^T{R}_n^T{R}_m(W_k{x}_m)=(W_q{x}_n{)}^T{R}_{m-n}(W_k{x}_m)$$

Because $R_n^T{R}_m=R_{m-n}$ (rotation matrices compose additively in angle), the attention score depends only on the relative position $m-n$, not the absolute positions. This is exactly the inductive bias we want.

For the full model dimension $d$, RoPE applies independent rotations to $d/2$ pairs of dimensions, each with a different frequency ${\theta }_i=10000^{-2i/d}$:

$$R_{\Theta ,n}=\left(\begin{array}{ccc}{R}_{n,1}& & \\ & \ddots & \\ & & R_{n,d/2}\end{array}\right)$$

The multi-frequency design encodes relative position at multiple scales, analogous to the original sinusoidal encoding but applied multiplicatively through rotation rather than additively.

RoPE became dominant because it gives a clean relative-position inductive bias without learned position parameters, integrates naturally into existing attention implementations, and tends to behave well in long-context regimes, especially when paired with explicit extrapolation strategies (e.g., NTK-aware scaling, YaRN) and careful training. This is best read as a strong default under modern constraints, not a proof of strict superiority over all alternatives in all regimes. The 2025 models experimenting with "NoPE" (no position encoding) in some layers, combined with RoPE in others, suggest the field is learning that different layers may benefit from different position treatments.

#SwiGLU: The Gating Advantage

The Gated Linear Unit (GLU) family improves FFN expressivity through multiplicative gating. SwiGLU specifically uses SiLU (Swish) as the activation:

$$\text{SwiGLU}(x,W_1,W_3,W_2)=(\text{SiLU}(x{W}_1)\odot x{W}_3)W_2$$

where $\text{SiLU}(x)=x\cdot \sigma (x)$ and $\sigma$ is the sigmoid function.

To understand why gating helps, consider what each component contributes:

1. $\text{SiLU}(x{W}_1)$: A nonlinearly transformed representation of the input
2. $x{W}_3$: A linear transformation of the input
3. Element-wise product: The linear path gates the nonlinear path

The gating mechanism allows the network to learn which features of the nonlinear transformation should be amplified or suppressed, conditioned on the input. This is more expressive than applying a fixed nonlinearity.

SwiGLU has three weight matrices ($W_1,W_3,W_2$) versus two for standard FFN ($W_1,W_2$). To maintain equivalent parameter count with expansion factor $e$:

Standard FFN: $2\cdot d\cdot ed=2e{d}^2$ parameters

SwiGLU with expansion $e^{\prime }$: $3\cdot d\cdot e^{\prime }d=3e^{\prime }{d}^2$ parameters

Setting these equal: $e^{\prime }=\frac{2e}{3}$. For $e=4$, we get $e^{\prime }=\frac{8}{3}\approx 2.67$.

The key hypothesis is that gating is worth more than width: trading hidden dimension for a gating mechanism improves expressivity more than the raw capacity lost. Empirically, this hypothesis is supported - SwiGLU consistently outperforms parameter-matched GeLU baselines in controlled comparisons [3]. The gating mechanism's input-dependent modulation allows the network to selectively amplify or suppress features, a form of dynamic computation that static nonlinearities cannot express.

SiLU also has favorable gradient flow properties. Unlike ReLU, it's smooth everywhere and has nonzero gradients for all $x$. In practice, SiLU/Swish often behaves comparably to GeLU while pairing naturally with GLU-style gating. The derivative:

$$\frac{d}{dx}\text{SiLU}(x)=\sigma (x)+x\sigma (x)(1-\sigma (x))=\sigma (x)(1+x(1-\sigma (x)))$$

is nonzero over a wide range (unlike ReLU's hard zero on $(-\infty ,0)$), which can improve gradient flow in practice; empirically, GLU-family MLPs often deliver better quality at similar parameter/FLOP budgets in transformer LMs.

#The MoE Routing Problem

Mixture-of-Experts architectures must solve a fundamental tension: tokens should be routed to the experts best suited for them, but all experts should be utilized to justify their parameter cost.

But MoE is prone to routing collapse. Without intervention, MoE training often converges to using only a few experts. Once an expert becomes slightly better for some token types, it receives more training signal, improving further, creating a feedback loop that starves other experts.

Traditionally, a load-balancing auxiliary loss is added:

$${\mathcal{L}}_{\text{balance}}=\alpha \cdot n\sum _{i=1}^n{f}_i\cdot P_i$$

where $f_i=\frac{1}{T}{\sum }_{t=1}^{T}1[\text{token }t\text{ routed to expert }i]$ and $P_i=\frac{1}{T}{\sum }_{t=1}^T{p}_i(x_t)$.

This encourages the router to spread probability mass and actual routing decisions evenly. The problem: it distorts the primary language modeling objective. The router is incentivized to balance load even when some experts are genuinely better for certain tokens.

DeepSeek's auxiliary-loss-free approach introduces a bias term $b_i$ for each expert that affects routing decisions but not expert weighting:

$$s_i=r_i(x)+b_i\text{(routing scores)}$$

Experts are selected by taking the top-$k$ scores under $s_i$ (the biased routing scores), but mixture weights are computed from the unbiased $r_i(x)$ over the selected set.

$$\text{output}=\sum _{i\in \text{top-}k}\frac{e^{r_i(x)}}{{\sum }_{j\in \text{top-}k}{e}^{r_j(x)}}{E}_i(x)$$

The biases $b_i$ are adjusted during training to maintain load balance (increase $b_i$ for underutilized experts), but because they don't affect the actual weighting, the model's output is determined purely by learned routing quality.

This is elegant: routing decisions include the bias (ensuring balance), but output computation excludes it (preserving training signal fidelity).

#QK-Normalization: Taming Attention Score Variance

Query-key normalization has emerged as a critical stability mechanism for large-scale training. The mathematical motivation stems from the statistics of high-dimensional dot products.

For query and key vectors $q,k\in {\mathbb{R}}^{d_k}$ with independent, zero-mean entries of variance ${\sigma }^2$, and assuming $q$ and $k$ are independent of each other, the dot product $q^{T}k$ has variance:

$$\text{Var}(q^{T}k)=d_k{\sigma }^4$$

These assumptions approximately hold at initialization but break down during training: entries become correlated, means drift from zero, and $q$-$k$ independence fails since both derive from the same input. The practical concern is not the initialization variance but drift - the learned norms of $q$ and $k$ can grow during training, increasing logit magnitudes and sharpening softmax distributions in ways the $\sqrt{d_k}$ scaling cannot prevent.

Even when $d_k$ is held constant, the learned norms of $q$ and $k$ can drift during training, increasing logit magnitudes and sharpening the softmax. This creates two problems:

1. Attention entropy collapse: Large-variance logits produce sharper softmax distributions, potentially collapsing to nearly one-hot attention patterns.
2. Numerical instability: Pre-softmax logits can grow large enough to cause overflow or severe precision loss.

The standard mitigation is the $\sqrt{d_k}$ scaling in attention:

$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

This scaling normalizes the dot-product variance under idealized assumptions (e.g., independent entries with fixed variance), but in trained models the norms and distributions of $q$ and $k$ can drift with depth, scale, and optimization, producing occasional logit blow-ups and overly peaky attention.

QK-normalization directly controls the vector norms:

$$\hat{q}=\frac{q}{\Vert q\Vert },\hat{k}=\frac{k}{\Vert k\Vert }$$

With strict L2-normalization and fixed scaling, the dot product is bounded $(|{\hat{q}}^{\top }\hat{k}|\le 1)$, which can prevent extreme logits. In practice, many implementations use RMSNorm-style normalization and may include learnable scales, so the benefit is better understood as controlling norm drift and reducing pathological logit growth, not as an absolute bound in all configurations.

The practical implementation often uses RMSNorm rather than L2 normalization, and may include learnable scale factors:

$$\hat{q}={\gamma }_q\cdot \text{RMSNorm}(q),\hat{k}={\gamma }_k\cdot \text{RMSNorm}(k)$$

Models using QK-norm (Gemma 3, OLMo 2, Qwen 3, Kimi K2, Trinity) report more stable training, especially at scale. The technique appears most beneficial for:

#Dataset of 53 Models Across Eight Years

The accompanying dataset documents architectural specifications for 53 transformer LLMs from June 2017 through December 2025. All entries were cross-referenced against public sources, with undisclosed information marked.

#Summary Statistics

A note on interpretation: this dataset is descriptive, not a controlled ablation study. Reported frequencies summarize what was adopted, but adoption reflects a mix of model quality, training stability, inference economics, and ecosystem path dependence (e.g., widely copied open baselines). We also note the following limitations:

• Selection criteria: Models were included based on (1) public technical report or paper, (2) significant discussion in the research community (ArXiv citations, blog coverage, downstream adoption), and (3) architectural novelty or influence. This tilts toward open-weight models and English-language publications.
• Family overlap: The dataset includes multiple versions of the same family (LLaMA, LLaMA 2, LLaMA 3). This inflates apparent convergence: if LLaMA 2 copies LLaMA's architecture, counting both overstates independent convergence. Family-level analysis would show fewer independent data points.
• Verification depth: Primary sources vary in detail. Some entries are cross-referenced against code (e.g., LLaMA, OLMo); others rely solely on papers that may omit implementation details.

Normalization convergence:

Position encoding evolution:

Activation functions:

MoE adoption:

Attention variant:

Block structure:

Vocabulary size trends:

#Dataset

Model	Date	Norm	Position	Activation	Attn	Block	MoE	Vocab	Stability
Original Transformer	2017-06	Post LayerNorm	Sinusoidal	ReLU	MHA	Serial	No	37K	None
GPT-1	2018-06	Post LayerNorm	Learned Abs	GeLU	MHA	Serial	No	40K	None
GPT-2	2019-02	Pre LayerNorm	Learned Abs	GeLU	MHA	Serial	No	50K	Modified init
T5	2019-10	Pre LayerNorm	Relative	ReLU	MHA	Serial	No	32K	None
GPT-3	2020-05	Pre LayerNorm	Learned Abs	GeLU	MHA	Serial	No	50K	Modified init; sparse attn
T5 v1.1	2020-10	Pre LayerNorm	Relative	GeGLU	MHA	Serial	No	32K	None
mT5	2020-10	Pre LayerNorm	Relative	GeGLU	MHA	Serial	No	250K	None
GPT-J	2021-05	Pre LayerNorm	RoPE	GeLU	MHA	Parallel	No	50K	None
LaMDA	2021-05	Pre LayerNorm	Relative	Gated-GeLU	MHA	Serial	No	32K	None
Gopher	2021-12	Pre RMSNorm	Relative	GeLU	MHA	Serial	No	32K	Low LR; grad clip
Chinchilla	2022-03	Pre RMSNorm	Relative	GeLU	MHA	Serial	No	32K	None
GPT-NeoX	2022-04	Pre LayerNorm	RoPE	GeLU	MHA	Parallel	No	50K	None
PaLM	2022-04	Pre LayerNorm	RoPE	SwiGLU	MHA	Parallel	No	256K	No biases; shared emb
OPT	2022-05	Pre LayerNorm	Learned Abs	ReLU	MHA	Serial	No	50K	Modified init
BLOOM	2022-11	Pre LayerNorm	ALiBi	GeLU	MHA	Serial	No	251K	Embedding LayerNorm
LLaMA	2023-02	Pre RMSNorm	RoPE	SwiGLU	MHA	Serial	No	32K	No biases
LLaMA 2	2023-07	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	32K	No biases
Qwen	2023-09	Pre RMSNorm	RoPE	SwiGLU	MHA	Serial	No	152K	None
Mistral 7B	2023-10	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	32K	Sliding window
Yi	2023-11	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	64K	None
DeepSeek	2024-01	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	102K	None
Mixtral	2024-01	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	8E/2act	32K	Load balance loss
OLMo	2024-02	Pre LayerNorm	RoPE	SwiGLU	MHA	Serial	No	50K	No biases
Gemma	2024-02	Pre RMSNorm	RoPE	GeGLU	MHA	Serial	No	256K	None
Phi-3	2024-04	Pre RMSNorm	RoPE	GeGLU	MHA	Serial	No	100K	Blocksparse attn
Reka Flash	2024-04	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	100K	None
Nemotron-4	2024-06	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	256K	None
GLM-4	2024-06	Pre RMSNorm	RoPE	SwiGLU	MHA	Serial	No	150K	No bias except QKV
Qwen 2	2024-07	Pre RMSNorm	RoPE+DCA	SwiGLU	GQA	Serial	No	152K	QKV bias
LLaMA 3 70B	2024-07	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	128K	None
LLaMA 3 405B	2024-07	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	128K	None
Mistral Large 2	2024-07	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	32K	-
Falcon 2	2024-07	Pre LayerNorm	RoPE	GeLU	MHA	Parallel	No	65K	FlashAttention-2
Gemma 2	2024-08	Pre+Post RMSNorm	RoPE	GeGLU	GQA	Serial	No	256K	Logit cap; local/global
Command R+	2024-09	Pre LayerNorm	RoPE	SwiGLU	GQA	Serial	No	256K	RAG opt
Qwen 2.5	2024-12	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	152K	QKV bias
Phi-4	2024-12	Pre RMSNorm	RoPE	GeGLU	MHA	Serial	No	100K	Synthetic data
DeepSeek V3	2024-12	Pre RMSNorm	RoPE	SwiGLU	MLA	Serial	256E+1/8act	128K	Aux-free; FP8
OLMo 2	2025-01	Pre RMSNorm	RoPE	SwiGLU	MHA	Serial	No	100K	QK-Norm; Z-Loss
MiniMax M2	2025-01	DeepNorm+RMSNorm	RoPE	SwiGLU	MHA	Serial	32E/2act	200K	Lightning Attention
DeepSeek R1	2025-01	Pre RMSNorm	RoPE	SwiGLU	MLA	Serial	256E+1/8act	128K	Aux-free; FP8
SmolLM2	2025-02	Pre RMSNorm	RoPE	SwiGLU	MHA	Serial	No	49K	Embedding tying
Gemma 3	2025-03	Pre+Post RMSNorm	RoPE	GeGLU	GQA	Serial	No	262K	QK-norm; 5:1 local/global
Command A	2025-03	Pre LayerNorm	RoPE+NoPE	SwiGLU	MHA	Parallel	No	255K	No biases; FP32 ops
Llama 4 Scout	2025-04	Pre RMSNorm	iRoPE	SwiGLU	GQA	Serial	16E+1/var	202K	MetaP init; FP8
Llama 4 Maverick	2025-04	Pre RMSNorm	iRoPE	SwiGLU	GQA	Serial	128E+1/var	202K	MetaP init; FP8; fusion
Qwen 3	2025-05	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	152K	QK-Norm; no QKV bias
Mistral Medium 3	2025-05	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	No	131K	-
GLM-4.5	2025-07	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	64E/4act	150K	QK-Norm; Muon
Kimi K2	2025-07	Pre RMSNorm	RoPE	SwiGLU	MLA	Serial	384E/8act	130K	QK-Clip; MuonClip
INTELLECT-3	2025-11	Pre RMSNorm	RoPE	SwiGLU	GQA	Serial	64E/4act	150K	Same as GLM-4.5-Air
Trinity Nano	2025-12	Depth-scaled RMSNorm	RoPE+NoPE	SwiGLU+Gated	GQA	Serial	128E/8act	32K	QK-norm; sigmoid route
Trinity Mini	2025-12	Depth-scaled RMSNorm	RoPE+NoPE	SwiGLU+Gated	GQA	Serial	128E+1/8act	32K	QK-norm; sigmoid route

#Patterns in the Data

LLaMA's February 2023 release marks a clear architectural boundary. Before: significant diversity in normalization, position encoding, and activation choices. After: near-universal adoption of the LLaMA recipe.

MoE configuration diversity persists. Unlike the converged dense architecture, MoE models show wide variation:

This diversity suggests MoE design is not yet settled. The optimal configuration likely depends on training budget, target inference cost, and use case.

Stability mechanisms cluster in 2024-2025: QK-normalization, logit capping, and specialized initialization appear almost exclusively in models from the last 18 months. This reflects both scaling to larger models where stability matters more and accumulated understanding of failure modes.

#Implications and Open Questions

#Practical takeaways: strong defaults, and when to deviate

A reasonable reading of 2017–2025 is not that architecture is "done", but that dense decoder-only transformers have a highly competitive default configuration under modern constraints (training stability, throughput on current accelerators, and inference KV-cache cost). Concretely:

#Interpreting convergence: what it does (and does not) imply

Architectural convergence is evidence of a strong shared basin of solutions, but it is not a proof of global optimality. It reflects both model-intrinsic considerations and strong external constraints.

Convergence reflects constraints and ecosystem dynamics. Choices that win often do so because they are good and easy to scale: they are stable at depth, efficient on GPUs/TPUs, compatible with fused kernels, and friendly to inference economics (especially KV-cache). Influential released baselines and reference implementations can accelerate standardization, creating path dependence even when multiple alternatives are viable.

But here's what convergence does not settle:

There is also a monoculture trade-off. A strong default accelerates progress and reproducibility, but it narrows exploration. This is particularly relevant for nonstandard settings (very long context, low-latency streaming, memory-limited deployment), where the best architecture might differ from the mainstream recipe.

Finally, a useful research posture would be to treat the consensus stack as a hard-to-beat baseline, and aim for claims of the form: "under explicit constraints X and evaluation Y, modification Z reliably improves metric M and does not regress N". That standard is what distinguishes robust architectural progress from recipe churn.

#Open Questions

#Conclusion

The eight-year trajectory from the original transformer to 2025 frontier systems follows a pattern of exploration → convergence → renewed divergence:

Era	Period	Pattern
I	2017-2019	Foundations established, immediate variations explored
II	2020-2022	Scaling drove efficiency innovations (RMSNorm, RoPE, SwiGLU)
III	2023-2024	LLaMA crystallized a reproducible recipe, standardization accelerated
IV	2024-2025	MoE emerged as dominant scaling axis, diversity returned

The dense-model convergence on a core bundle (pre-norm + RMSNorm + RoPE + SwiGLU, often paired with MQA/GQA-style KV sharing and reduced bias usage) suggests a robust, highly competitive basin of solutions under today’s constraints. It is evidence of what tends to work when optimizing simultaneously for stability, throughput on current accelerators, and inference cost, while also benefiting from an ecosystem of shared implementations and kernels. It is not, by itself, a proof of global optimality.

At the same time, the remaining variation (MoE routing and expert design, long-context attention patterns, and an increasing number of explicit stability interventions) highlights where the architecture is still actively adapting. These choices look less like settled convention and more like responses to new failure modes that appear at larger scale and longer context.

If there is a meta-lesson in the 2017 → 2025 shift, it is how quickly "reasonable defaults" can change once scale and constraints change. Many early design choices (post-norm, learned absolute positions, ReLU) were not wrong so much as eventually outcompeted. The next shift may come from long-context regimes, different hardware constraints, or architectures that change the attention/computation trade-off entirely.

---

This analysis is inspired by Tatsunori Hashimoto's lecture on architectures and hyperparameters in Stanford CS336 (April 2025).

---